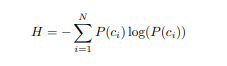Curve Fitting and Error Function
Salah satu bentuk utility function untuk model matematis bernama error function. Fungsi ini sudah banyak diceritakan pada bab-bab sebelumnya secara deskriptif. Mulai bab ini, kamu akan mendapatkan pengertian lebih jelas secara matematis.Error function paling mudah dijelaskan dalam permasalahan regresi. Diberikan (x, y) ∈ R sebagai random variable. Terdapat sebuah fungsi f(x) → y, yang memetakan x ke y, berbentuk seperti pada Gambar 5.1. sekarang fungsi f(x) tersebut disembunyikan (tidak diketahui), diberikan contoh-contoh pasangan (xi , yi); i = 1, 2, ..., 6 adalah titik pada dua dimensi (titik sampel), seperti lingkaran berwarna biru. Tugasmu adalah untuk mencari tahu f(x)! Dengan kata lain, kita harus mampu memprediksi sebuah bilangan riil y, diberikan suatu x.
Kamu berasumsi bahwa fungsi f(x) dapat diaproksimasi dengan fungsi linear g(x) = xw + b. Artinya, kamu ingin mencari w dan b yang memberikan nilai sedemikian sehingga g(x) mirip dengan f(x). w adalah parameter sementara b adalah bias. Anggap kamu sudah berhasil melakukan pendekatan dan 5 Model Linear.
 |
| Gambar 5.1 Contoh Fungsi Sigmoid |
menghasilkan fungsi linear g(x); seperti Gambar 5.2 (garis berwarna hijau). Akan tetapi, fungsi approksimasi ini tidak 100% tepat sesuai dengan fungsi aslinya (ini perlu ditekankan)1 . Jarak antara titik biru terhadap garis hijau disebut error.
 |
| Gambar 5.2 Pendekatan fungsi Signoid |
Salah satu cara menghitung error fungsi g(x) adalah menggunakan squared error function dengan bentuk konseptual pada persamaan 5.1. Estimasi terhadap persamaan tersebut disajikan dalam bentuk diskrit pada persamaan 5.2. (xi , yi) adalah pasangan training data (input - desired output). Nilai squared error dapat menjadi tolak ukur untuk membandingkan kinerja suatu learning machine (model). Secara umum, bila nilainya tinggi, maka kinerja dianggap relatif buruk; sebaliknya bila rendah, kinerja dianggap relatif baik. Hal ini sesuai dengan konsep intelligent agent [5].
Binary Classification
Binary classification adalah mengklasifikasikan data menjadi dua kelas (binary). Contoh model linear sederhana untuk binary classification diberikan pada persamaan 5.6. Perhatikan, pada persamaan 5.6, suatu data direpresentasikan sebagai feature vector x, dan terdapat bias2 b. Klasifikasi dilakukan dengan melewatkan data pada fungsi yang memiliki parameter. Fungsi tersebut menghitung bobot setiap fitur pada vektor dengan mengalikannya dengan parameter (dot product). Persamaan 5.6 dapat ditulis kembali sebagai persamaan 5.7, dimana xi merupakan elemen ke-i dari vektor x. Fungsi ini memiliki range [−∞, ∞]. Pada saat ini, kamu mungkin bingung. Bagaimana mungkin fungsi regresi yang menghasilkan nilai kontinu digunakan untuk klasifikasi kelas kategorial. Kita dapat menggunakan thresholding, atau dengan memberikan batas nilai tertentu. Misal, bila f(x) > threshold maka dimasukkan ke kelas pertama; dan sebaliknya f(x) ≤ threshold dimasukkan ke kelas kedua. Threshold menjadi bidang pembatas antara kelas satu dan kelas kedua (decision boundary, Gambar 5.3). Pada umumnya, teknik threshold diterapkan dengan menggunakan fungsi sign (sgn, Gambar 5.4) untuk merubah nilai fungsi menjadi [−1, 1] sebagai output (persamaan 5.8); dimana −1 merepresentasikan input dikategorikan ke kelas pertama dan nilai 1 merepresentasikan input dikategorikan ke kelas kedua.Seperti halnya fungsi regresi, kita juga dapat menghitung performa binary classifier sederhana ini menggunakan squared error function (umumnya menggunakan akurasi), dimana nilai target fungsi berada pada range [−1, 1]. Secara sederhana, model binary classifier mencari decision boundary, yaitu garis (secara lebih umum, hyperplane) pemisah antara kelas satu dan lainnya. Sebagai contoh, garis hitam pada Gambar 5.3 adalah decision boundary.
Log-linear Binary Classification
Pada subbab sebelumnya, telah dijelaskan fungsi binary classifier memetakan data menjadi nilai [−1, 1], dengan −1 merepresentasikan kelas pertama dan 1 merepresentasikan kelas kedua. Tidak hanya kelas yang berkorespondensi,5.3 Log-linear Binary Classification
 |
| Gambar 5.3 Contoh Decision Boundary |
 |
| Gambar 5.4 Fungsi Sign |
Fungsi sign kita juga terkadang ingin tahu seberapa besar peluang data tergolong pada kelas tersebut. Salah satu alternatif adalah dengan menggunakan fungsi sigmoid dibanding fungsi sign untuk merubah nilai fungsi menjadi [0, 1] yang merepresentasikan peluang data diklasifikasikan sebagai kelas tertentu (1 - nilai peluang, untuk kelas lainnya). Konsep ini dituangkan menjadi persamaan 5.9, dimana y merepresentasikan probabilitas input x digolongkan ke kelas tertentu, x merepresentasikan data (feature vector ), dan b merepresentasikan bias. Ingat kembali materi bab 4, algoritma Naive Bayes melakukan hal serupa3 . Hasil fungsi sigmoid, apabila di-plot maka akan berbentuk seperti Gambar 5.1 (berbentuk karakter “S”).
Menggunakan nilai peluang untuk klasifikasi 64 5 Model Linear Perhatikan, persamaan 5.9 juga dapat diganti dengan persamaan 5.10 yang dikenal juga sebagai fungsi logistik.
y = logistik(f(x)) = e (x·w+b) 1 + e (x·w+b) (5.10)
Nilai y ini diasosiasikan dengan suatu kelas. y adalah nilai probabilitas data masuk ke suatu kelas. Sebagai contoh, kita ingin nilai y = 1 apabila data cocok masuk ke kelas pertama dan y = 0 apabila masuk ke kelas kedua. Ketika fungsi machine learning menghasilkan nilai berbentuk probabilitas, kita dapat menggunakan cross entropy sebagai utility function. Persamaan 5.11 adalah cara menghitung cross entropy, dimana P(ci) melambangkan probabilitas input diklasifikasikan ke kelas ci dan N melambangkan banyaknya kelas. Untuk binary classification, P(c1) = 1 − P(c2).
Kita ingin meminimalkan nilai cross entropy untuk model pembelajaran mesin yang baik. Ingat kembali materi teori informasi, nilai entropy yang rendah melambangkan distribusi tidak uniform. Sementara, nilai entropy yang tinggi melambangkan distribusi lebih uniform. Artinya, nilai cross entropy yang rendah melambangkan high confidence saat melakukan klasifikasi. Kita ingin model kita sebiasa mungkin menghasilkan output bernilai 1 untuk mendiskriminasi seluruh data yang masuk ke kelas pertama, dan 0 untuk kelas lainnya. Dengan kata lain, model dapat mendiskriminasi data dengan pasti. Dengan analogi, kita ingin fungsi logistik kita berbentuk semirip mungkin dengan fungsi sign untuk high confidence. Cross entropy bernilai tinggi apabila perbedaan nilai probabilitas masuk ke kelas satu dan kelas lainnya tidak jauh, e.g., P(c1) = 0.6 & P(c2) = 0.4. Semakin rendah nilai cross entropy, kita bisa meningkatkan “keyakinan” kita terhadap kemampuan klasifikasi model pembelajaran mesin, yaitu perbedaan nilai probabilitas masuk ke kelas satu dan kelas lainnya tinggi, e.g., P(c1) = 0.8 & P(c2) = 0.2.
Multi-class Classification
Subbab ini akan membahas tentang multi-class classification, dimana terdapat lebih dari dua kemungkinan kelas. Terdapat himpunan kelas C beranggotakan {c1, c2, . . . , cK}. Untuk suatu data dengan representasikan feature vector -nya, kita ingin mencari tahu kelas yang berkorespondesi untuk data tersebut. Contoh permasalahan ini adalah mengklasifikasi gambar untuk tiga kelas: apel, jeruk, atau mangga. Cara sederhana adalah memiliki tiga buah vektor parameter dan bias berbeda, wapel, wjeruk, wmangga, dan bias b{apel,jeruk,mangga}. Untuk menentukan suatu data masuk ke kelas mana, kita 5.4 Multi-class Classification 65 dapat memprediksi skor tertinggi yang diberikan oleh operasi feature vector terhadap masing-masing vektor parameter. Konsep matematisnya diberikan pada persamaan 5.12, dimana ˆc adalah kelas terpilih (keputusan), yaitu kelas yang memiliki nilai tertinggi. C melambangkan himpunan kelas.Tiga set parameter wci dapat disusun sedemikian rupa sebagai matriks W ∈ R d×3 , dimana d adalah dimensi feature vector (x ∈ R 1×d ). Demikian pula kita dapat susun bias menjadi vektor b ∈ R 1×3 berdimensi tiga. Dengan demikian, persamaan 5.12 dapat ditulis kembali sebagai persamaan 5.13, dimana c adalah vektor yang memuat nilai fungsi terhadap seluruh kelas. Kita memprediksi kelas berdasarkan indeks elemen c yang memiliki nilai terbesar (Persamaan 5.14). Analogika, seperti memilih kelas dengan nilai likelihood tertinggi.
Seperti yang diceritakan pada subbab berikutnya, kita mungkin juga tertarik dengan probabilitas masing-masing kelas, bukan hanya likelihood-nya. Kita dapat menggunakan fungsi softmax 4 untuk hal ini. Fungsi softmax mentransformasi c agar jumlah semua nilainya berada pada range [0, 1]. Dengan itu, c dapat diinterpretasikan sebagai distribusi probabilitas. Konsep ini dituangkan pada persamaan 5.15, dimana ci adalah elemen vektor ke-i, melambangkan probabilitas masuk ke kelas ke-i.
Karena output fungsi berupa distribusi probabilitas, kita juga dapat menghitung loss menggunakan cross entropy. Seperti yang sudah dijelaskan sebelumnya pada binary classification, kita ingin hasil perhitungan cross entropy sekecil mungkin karena meminimalkan nilai cross entropy meningkatkan confidence saat proses klasifikasi. Hal ini dapat dianalogikan dengan jargon “winner takes it all”. Sebagai ilustrasi, lihatlah Gambar 5.5. Kita ingin agar bentuk distribusi probabilitas output kelas (c) condong ke salah satu sisi saja.
Multi-label Classification
Seperti halnya multi-class classification, kita dapat mendekomposisi multilabel classification menjadi beberapa binary classifier (analogi persamaan 5.12). Yang membedakan multi-class dan multi-label adalah output c. Pada multiclass classification, ci ∈ c melambangkan probabilitas suatu instans masuk ke kelas ci . Keputusan akhir class assignment didapatkan dari elemen c dengan nilai terbesar. Untuk multi-label classification nilai ci ∈ c melambangkan apakah suatu kelas masuk ke kelas ci atau tidak. Bedanya, kita boleh mengassign lebih dari satu kelas (atau tidak sama sekali). Misal ci ≥ 0.5, artinya kita anggap model tersebut layak masuk ke kelas ci , tanpa harus membandingannya dengan nilai cj (i 6= j) lain. Inilah yang dimaksud dengan prinsip mutual exclusivity. Perhatikan Gambar 5.8 sebagai ilustrasi, dimana “1” melambangkan class assignment.Sekali lagi, nilai ci ∈ c bernilai [0, 1] tetapi keputusan klasifikasi apakah suatu kelas masuk ke dalam ci tidak bergantung pada nilai cj (i 6= j) lainnya. Berdasarkan prinsip mutual exclusivity, output c pada classifier 5.7 tidak ditransformasi menggunakan softmax. Pada umumnya, multi-label classifier melewatkan output c ke dalam fungsi sigmoid. Dengan demikian, persamaan 5.15 diganti menjadi persamaan 5.16 pada multi-label classifier.
Berhubung cara menginterpretasikan output berbeda dengan multi-class classification, cara evaluasi kinerja juga berbeda. Ada dua pendekatan evaluasi pada multi-label classification. Pertama, kita evaluasi kinerja binary classification untuk setiap kelas. Pada pendekatan ini, seolah-olah kita memiliki banyak binary classifiers untuk melakukan klasifikasi. Kedua, kita dapat mengevaluasi kinerja multi-label classification itu sendiri. Perhatikan Gambar 5.9! Pendekatan pertama ibarat membandingkan kolom desired output untuk masing-masing kelas dengan prediction yang berkorespondensi. Pada pendekatan kedua, kita membandingkan baris untuk tiap-tiap prediksi (seperti biasa). Saat kita membandingkan tiap-tiap baris prediksi, kita bisa jadi mendapatkan prediksi tipe exact match (seluruh prediksi sama dengan desired output), partially correct (sebagian prediksi sama dengan desired output) atau complete incorrect (tidak ada prediksi yang sama dengan desired output). Dengan ini, evaluasi multi-label classification relatif lebih kompleks dibanding multi-class classification biasa. Untuk mendapatkan multi-label classification accuracy, kita dapat menghitung berapa seberapa banyak exact match dibandingkan jumlah instans (walaupun hal ini terlalu ketat). Selain itu, kita dapat menghitung loss menggunakan cross entropy untuk mengevaluasi kinerja saat melatih multi-label classifier, layaknya multi-class classifier.
Pembelajaran sebagai Permasalahan Optimisasi
Salah satu tujuan dari pembelajaran (training) adalah untuk meminimalkan error sehingga kinerja learning machine (model) diukur oleh squared error. Dengan kata lain, utility function adalah meminimalkan squared error. Secara lebih umum, kita ingin meminimalkan/memaksimalkan suatu fungsi yang dijadikan tolak ukur kinerja (utility function), diilustrasikan pada persamaan 5.17, dimana θ adalah learning parameter 5 , dan L adalah loss function. Perubahan parameter dapat menyebabkan perubahan loss. Karena itu, loss function memiliki θ sebagai parameternya.dimana ˆθ adalah nilai parameter paling optimal. Perhatikan, “arg min” dapat juga diganti dengan “arg max” tergantung optimisasi apa yang ingin dilakukan.
Model Linear Sekarang, mari kita hubungkan dengan contoh yang sudah diberikan pada subbab sebelumnya. Kita coba melakukan estimasi minimum squared error, dengan mencari nilai learning parameters w yang meminimalkan nilai error pada model linear (persamaan 5.18)6 . Parameter model pembelajaran mesin biasanya diinisialisasi secara acak atau menggunakan distribusi tertentu. Terdapat beberapa cara untuk memimalkan squared error. Yang penulis akan bahas adalah stochastic gradient descent method 7 . Selanjutnya apda buku ini, istilah gradient descent, gradient-based method dan stochastic gradient descent mengacu pada hal yang sama.
Bayangkan kamu sedang berada di puncak pegunungan. Kamu ingin mencari titik terendah pegunungan tersebut. Kamu tidak dapat melihat keseluruhan pegunungan, jadi yang kamu lakukan adalah mencari titik terendah (lokal) sejauh mata memandang, kemudian menuju titik tersebut dan menganggapnya sebagai titik terendah (global). Layaknya asumsi sebelumnya, kamu juga turun menuju titik terendah dengan cara melalui jalanan dengan kemiringan paling tajam, dengan anggapan bisa lebih cepat menuju ke titik terendah [9]. Sebagai ilustrasi, perhatikan Gambar 5.10!
Stochastic Gradient Descent Jalanan dengan kemiringan paling tajam adalah −grad E(w), dimana E(w) adalah nilai error saat model memiliki parameter w. Dengan definisi grad E(w) diberikan pada persamaan 5.19 dan persamaan 5.20, dimana wi adalah nilai elemen vektor ke-i.
Batasan Model Linier
Model linear, walaupun mudah dimengerti, memiliki beberapa batasan. Ada
dua batasan paling kentara [17]: (1) additive assumption dan (2) linear assumption.
Additive assumption berarti model linear menganggap hubungan antara
input dan output adalah linear. Artinya, perubahan nilai pada suatu fitur xi
pada input x akan merubah nilai output secara independen terhadap fitur
lainnya. Hal ini terkadang berakibat fatal karena fitur satu dan fitur lainnya
dapat berinteraksi satu sama lain. Solusi sederhana untuk permasalahan ini
adalah dengan memodelkan interaksi antar-fitur, seperti diilustrasikan pada
persamaan 5.24 untuk input yang tersusun atas dua fitur.
Dengan persamaan 5.24, apabila x1 berubah, maka kontribusi x2 terhadap
output juga akan berubah (dan sebaliknya). Akan tetapi, seringkali interaksi
antar-fitur tidaklah sesederhana ini. Misal, semua fitur berinteraksi satu sama
lain secara non-linear.
Linear assumption berarti perubahan pada suatu fitur xi mengakibatkan
perubahan yang konstan terhadap output, walaupun seberapa besar/kecil nilai
xi tersebut. Seringkali, perubahan pada output sesungguhnya bergantung juga
pada nilai xi
itu sendiri, bukan hanya pada delta xi
. Solusi sederhana untuk
permasalahan ini adalah memodelkan fungsi linear sebagai fungsi polinomial
dengan orde (M) tertentu, diilustrasikan pada persamaan 5.25. Akan tetapi,
pemodelan inipun tidaklah sempurna karena rawan overfitting.
Asumsi yang sebelumnya dijelaskan pada pemodelan polinomial, dapat diekstensi menjadi generalized additive model (GAM) untuk mengatasi masalah
linear assumption, seperti diilustrasikan pada persamaan 5.26 [17]. Artinya,
kita melewatkan setiap fitur xi pada suatu fungsi gi
, sehingga delta xi tidak
mengakibatkan perubahan yang konstan terhadap output. Ekstensi ini dapat
memodelkan hubungan non-linear antara fitur dan output.
Tetapi, GAM masih saja memiliki batasan additive assumption. Dengan
demikian, interaksi antar-variabel tidak dapat dimodelkan dengan baik.
Overfitting dan Underfitting
Tujuan machine learning adalah membuat model yang mampu memprediksi
data yang belum pernah dilihat (unseen instances) dengan tepat; disebut
sebagai generalisasi (generalization). Seperti yang sudah dijelaskan pada bab
pertama, kita dapat membagi dataset menjadi training, development, dan testing dataset. Ketiga dataset ini berasal dari populasi yang sama dan dihasilkan
oleh distribusi yang sama (identically and independently distributed). Dalam
artian, ketiga jenis dataset mampu melambangkan (merepresentasikan) karakteristik yang sama8
. Dengan demikian, kita ingin loss atau error pada training, development, dan testing bernilai kurang lebih bernilai sama (i.e., kinerja
yang sama untuk data dengan karakteristik yang sama). Akan tetapi, underfitting dan overfitting mungkin terjadi.
Underfitting adalah keadaan ketika kinerja model bernilai buruk baik pada
training atau development maupun testing data. Overfitting adalah keadaan
ketika kinerja model bernilai baik untuk training tetapi buruk pada unseen
data. Hal ini diilustrasikan pada Gambar 5.14. Underfitting terjadi akibat
model yang terlalu tidak fleksibel, yaitu memiliki kemampuan yang rendah untuk mengestimasi variasi fungsi. Sedangkan, overfitting terjadi ketika
model terlalu fleksibel, yaitu memiliki kemampuan yang terlalu tinggi untuk
mengestimasi banyak fungsi atau terlalu mencocokkan diri terhadap training data. Perhatikan kembali Gambar 5.14, dataset asli diambil (sampled)
dari fungsi polinomial orde-3. Model underfitting hanya mampu mengestimasi dalam orde-1 (kemampuan terlalu rendah), sedangkan model overfitting
mampu mengestimasi sampai orde-9 (kemampuan terlalu tinggi).
Apabila kita gambarkan grafik kinerja terhadap konfigurasi model (model
order ), fenomena underfitting dan overfitting dapat diilustrasikan seperti
Gambar 5.15. Model yang ideal adalah model yang memiliki kinerja yang baik pada training, development, dan testing data. Artinya, kita ingin perbedaan kinerja model pada berbagai dataset bernilai sekecil mungkin. Untuk
menghindari overfitting atau underfitting, kita dapat menambahkan fungsi
noise/bias (selanjutnya disebut noise/bias saja) dan regularisasi (subbab 5.9).
Hal yang paling perlu pembaca pahami adalah untuk jangan merasa senang
ketika model machine learning yang kamu buat memiliki kinerja baik pada
training data. Kamu harus mengecek pada development dan testing data, serta
memastikan kesamaan karakteristik data, e.g., apakah training dan testing data benar diambil dari distribusi yang sama. Selain itu, kamu juga harus
memastikan apakah data yang digunakan mampu merepresentasikan kompleksitas pada permasalahan asli/dunia nyata. Sering kali, dataset yang digunakan pada banyak eksperimen adalah toy dataset, semacam simplifikasi
permasalahan dengan jumlah instans yang relatif sedikit. Kamu harus hatihati terhadap overclaiming, i.e., menjustifikasi model dengan performa baik
pada toy dataset sebagai model yang baik secara umum.